Low pass FIR filter
Intro
Some fast intro to low pass filters. Let's say this is notes is just to get into low pass filters without detailed explanations. Just play with tools like Octave and get sense of how it works. Well here is used Inglish so your eyes gona bleed.
So what is low-pass filter? In DSP its algo that can filter some array of values or data and reduce amount of high frequency fluctuations. For example if you recording movements of your hand and your hand is shaking(shaking very fast), low pass filter can "remove" that from your recorded data.
If you have recording sound were you noticed that flying mosquito is recorded then with is you can reduce noise from mosquito in recorded sound.
If you just use filter as a function then main params is how good are your filter and cut-off frequency. Good filter have higher number of filter coefficients with are determined from filter order. Cut-off frequency is set to normalised values html from 0.0 ... 1.0. Set them according which part should be filtered.
Octave examples
Draw first filter characteristics
1 | fir1([filter order],[cutoff freq])
|
Draw in Octave simple 40th order filter, as in Octave example
1 | freqz (fir1 (40, 0.3));
|
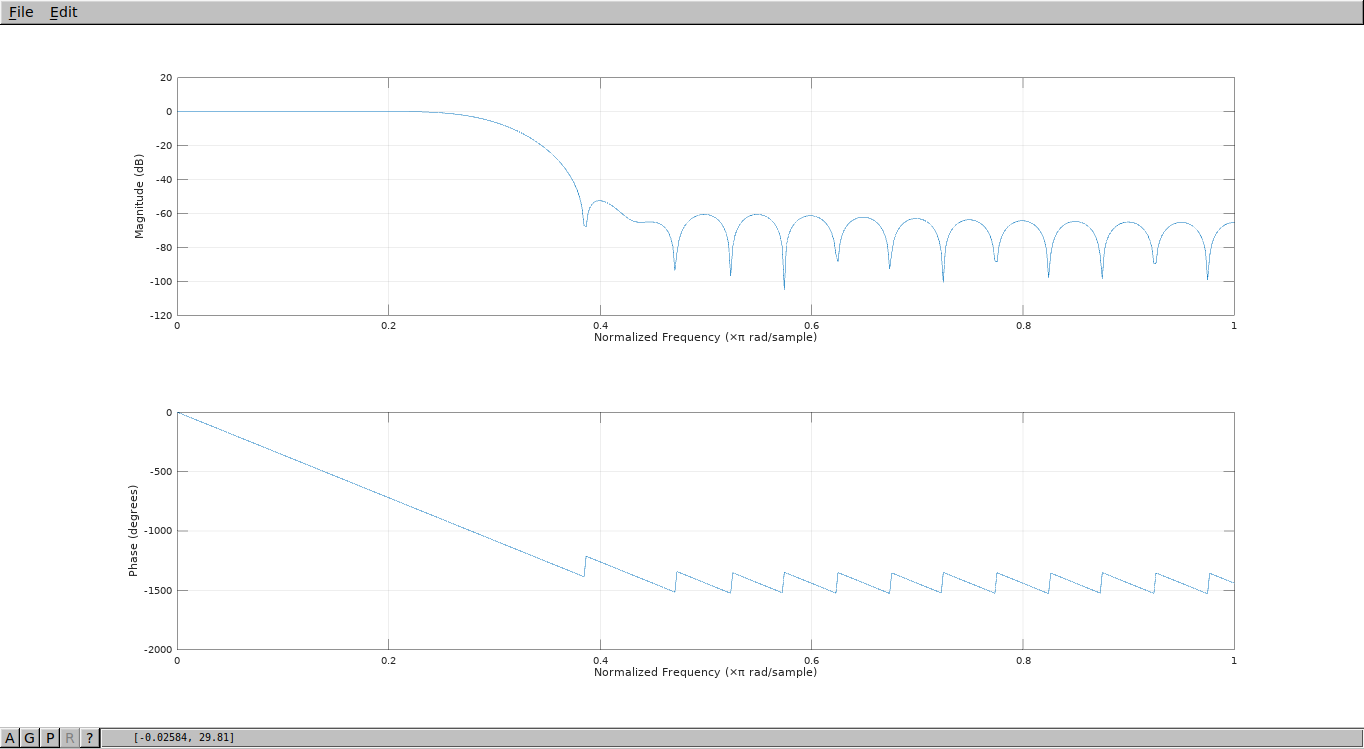
Play with first param of fir1 and you will see how it affects characteristics of filter. Try filter increase filter order from 1,2,3,4 and then go to higher numbers like 100.
You will see 2 pictures. First picture show frequency response of filter.
Good low-pass digital filter should have right side lower than left side of picture. And transition from left to right should be sharp as possible. We can see visually if this requirements are met. If filter order is increased more sharp transition becomes.
Second picture showing phase response. Well for now it's not so "important".
Create signal and filter it
Let's create some signal from couple of frequencies, like 100,400,750,1000,1200,1500 then let's do FFT to see what we have.
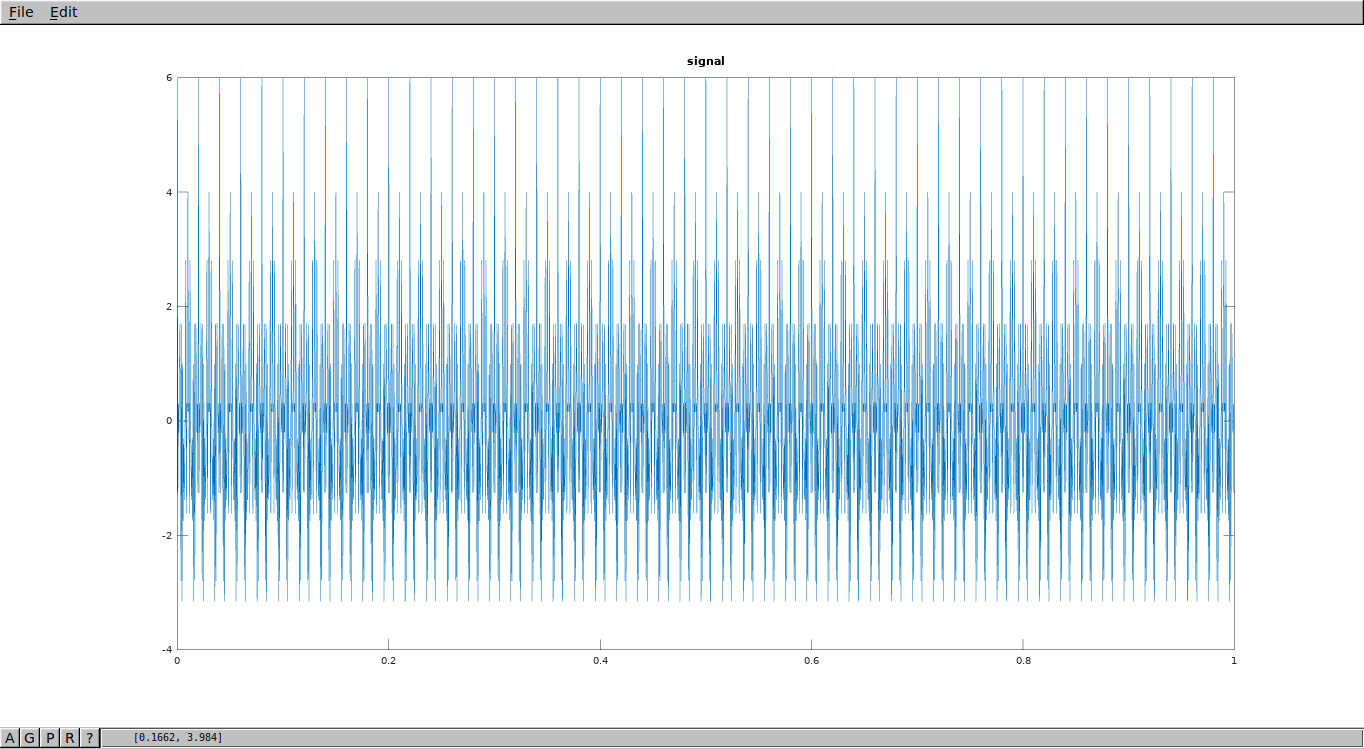 Low FIR pass-filer
Low FIR pass-filer
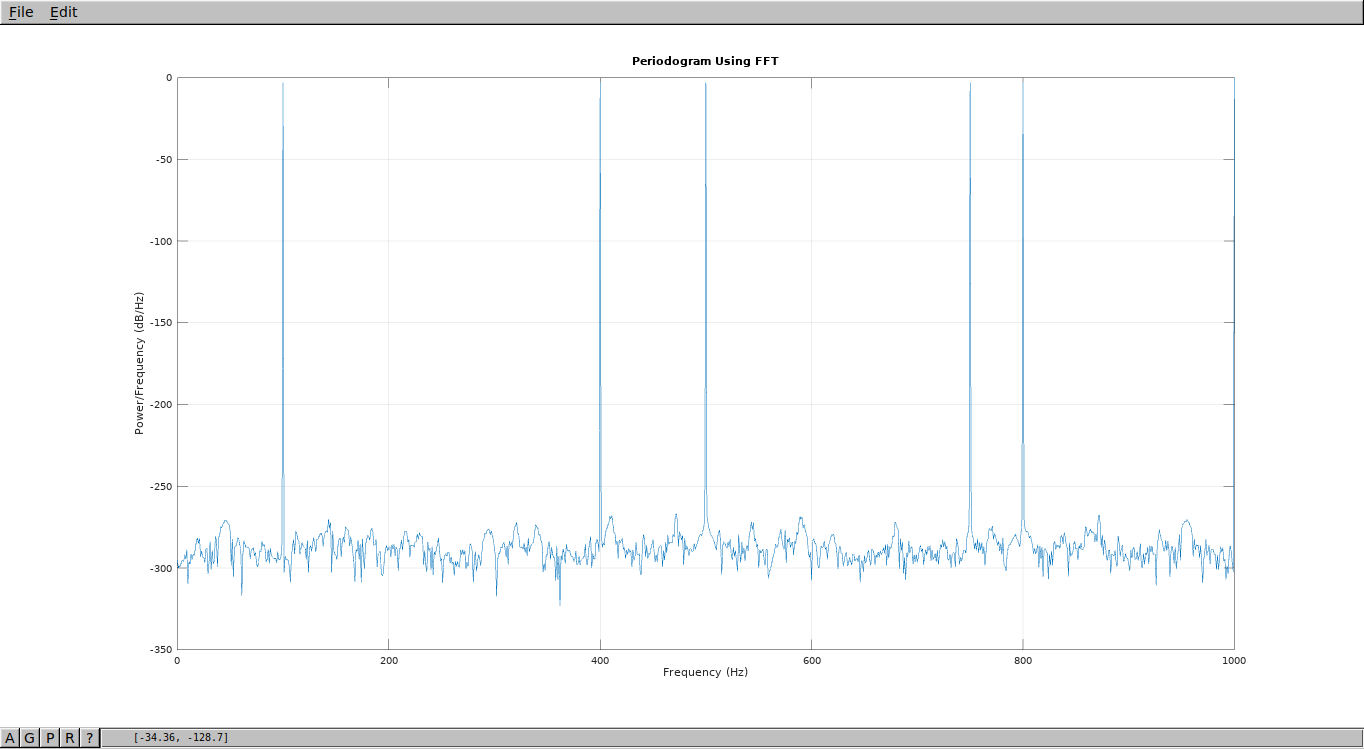
Programm
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | Fs = 2000;
t = 0:1/Fs:1-1/Fs;
x = cos(2*pi*100*t) + cos(2*pi*400*t) + cos(2*pi*750*t) \
+ cos(2*pi*1000*t) + cos(2*pi*1200*t) + cos(2*pi*1500*t);
N = length(x);
xdft = fft(x);
xdft = xdft(1:N/2+1);
psdx = (1/(Fs*N)) * abs(xdft).^2;
psdx(2:end-1) = 2*psdx(2:end-1);
freq = 0:Fs/length(x):Fs/2;
figure(1)
plot(freq,10*log10(psdx))
grid on
title('Periodogram Using FFT')
xlabel('Frequency (Hz)')
ylabel('Power/Frequency (dB/Hz)')
|
Lets filter out with cut-off frequency 1000kHz. Should get rid of 1000,1200,1500 frequencies in resulting FFT.
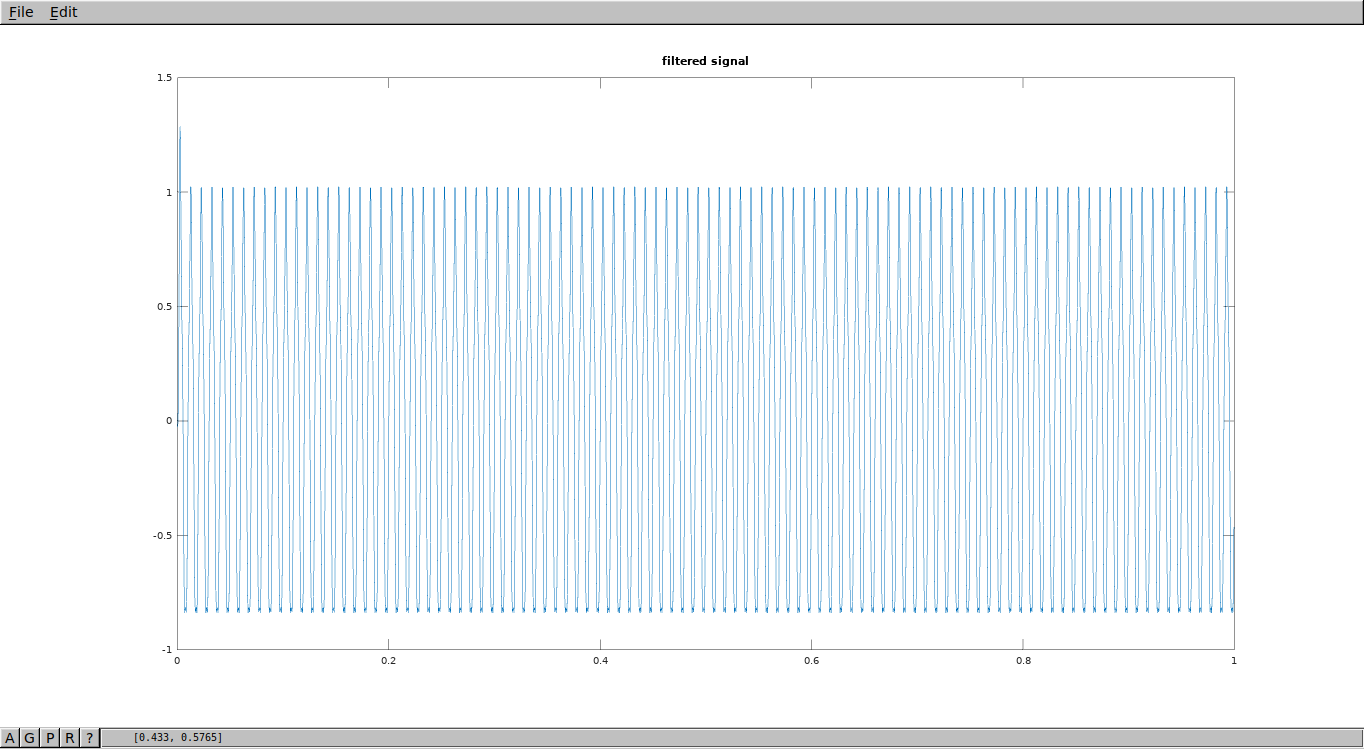
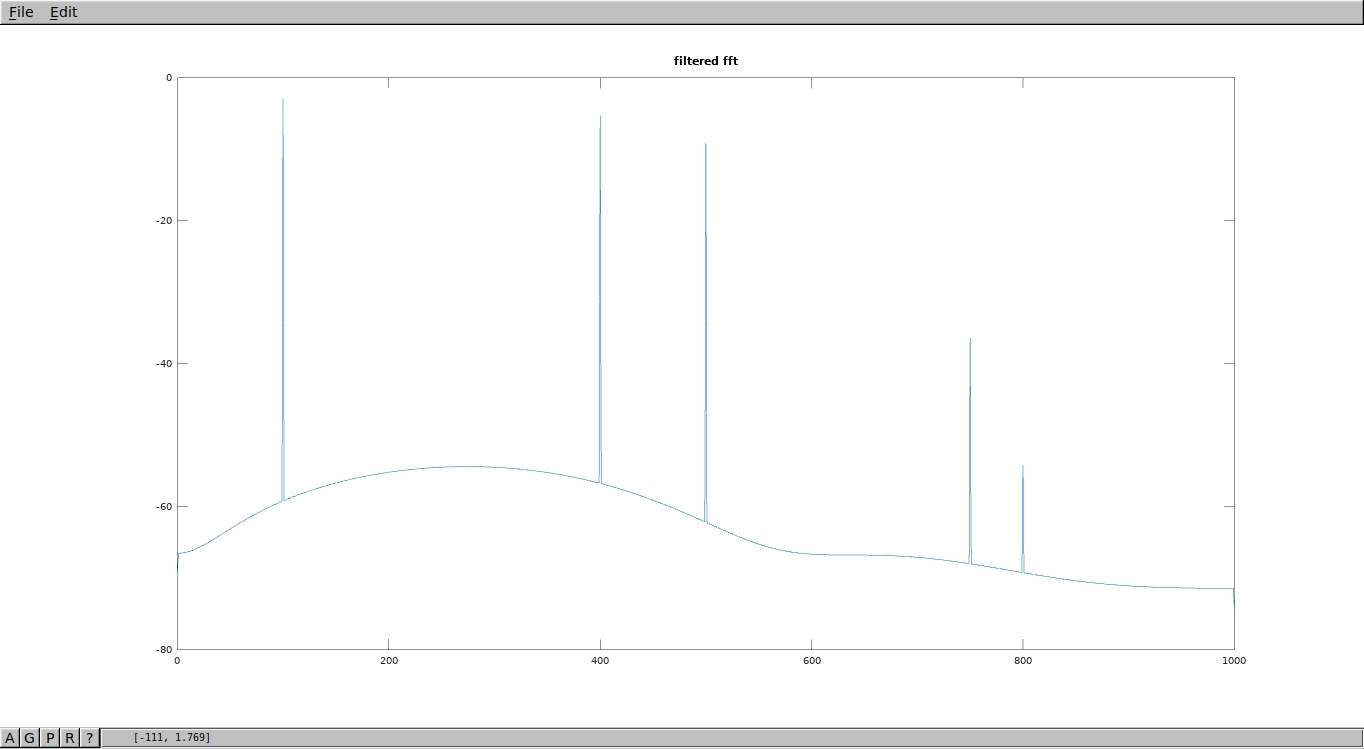
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | %filter
%sampling frequency
Fs = length(x);
Fnyq = Fs/2;
fc = 1000;
fdev = 20;
%[b,a]=butter(8, [900/Fs,1100/Fs]);
hc = fir1(41,fc/Fs);
f_filt = filter( hc, 1, x );
N = length(f_filt);
xdft = fft(f_filt);
xdft = xdft(1:N/2+1);
psdx = (1/(Fs*N)) * abs(xdft).^2;
psdx(2:end-1) = 2*psdx(2:end-1);
freq = 0:Fs/length(x):Fs/2;
figure(2);
plot( freq,10*log10(psdx) );
title("filtered fft");
figure(3);
freqz(fir1(41,0.5));
|
Calculate coefficients
Code example
Octave allows to see what filter properties is, also can choose appropriate filter type. Find how precise filter should be. And also test data on some signal sample. Now lets implement that with C.
Define FIR filter coefficients
1 2 3 4 5 6 7 8 | #define FIR_SIZE 12
double fir_coef[FIR_SIZE] =
{
-0.0044384, -0.0041841, 0.0130183, 0.0746628,
0.1720210, 0.2489204, 0.2489204, 0.1720210,
0.0746628, 0.0130183, -0.0041841, -0.0044384
};
|
FIR Filter
Applying filter coefficients to input signal, place where filtering is happening.
$$y(n) = \sum_{k=0}^{N-1}h(k)x(n-k) $$
1 2 3 4 | for (k=0;k<filter_length;k++)
{
acc += (*coeffp++)*(*inputp--);
}
|
Full programm
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 | #include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define FIR_SIZE 12
double fir_coef[FIR_SIZE] =
{
-0.0044384, -0.0041841, 0.0130183, 0.0746628,
0.1720210, 0.2489204, 0.2489204, 0.1720210,
0.0746628, 0.0130183, -0.0041841, -0.0044384
};
#define MAX_INPUT_LEN 80
#define BUFFER_LEN (FIR_SIZE-1+MAX_INPUT_LEN)
double insamp[BUFFER_LEN];
int fir1filter(double *coeffs, double *input, double *output,
int length, int filter_length)
{
double acc;
double *coeffp;
double *inputp;
int n;
int k;
memcpy(&insamp[filter_length-1], input, length*sizeof(double));
for (n=0; n<length; n++)
{
coeffp = coeffs;
inputp = &insamp[filter_length - 1 + n];
acc = 0;
for (k=0;k<filter_length;k++)
{
acc += (*coeffp++)*(*inputp--);
}
output[n] = acc;
}
memmove(&insamp[0], &insamp[length], (filter_length-1)*sizeof(double));
}
int main(int argc, char **argv)
{
int i,j;
double input[MAX_INPUT_LEN];
double output[MAX_INPUT_LEN];
int argc_len;
argc_len = argc - 1;
for (i=1;i<argc%(MAX_INPUT_LEN+1);i++)
{
input[i-1]=atof(argv[i]);
}
fir1filter(fir_coef, input, output, argc_len, FIR_SIZE);
for (i=0; i<argc_len; i++)
{
printf("%f ", output[i]);
}
printf("\n");
return 0;
}
|
Using program
1 2 | ./lpf1 1.0 0.0 0.0 0.0 0.0
-0.004438 -0.004184 0.013018 0.074663 0.172021
|
Links
- https://en.wikipedia.org/wiki/Low-pass_filter
- http://www.tedpavlic.com/teaching/osu/ece209/lab3_opamp_FO/lab3_opamp_FO_phase_shift.pdf
- https://octave.sourceforge.io/signal/function/fir1.html
- https://tty1.net/blog/2009/filters-with-gnu-octave_en.html8
- https://www.dsprelated.com/freebooks/sasp/Lowpass_Filter_Design_Specifications.html
- https://gist.github.com/akiatoji/5649907
- https://www.allaboutcircuits.com/technical-articles/design-of-fir-filters-design-octave-matlab/
- https://sestevenson.wordpress.com/implementation-of-fir-filtering-in-c-part-1/
- http://www.labbookpages.co.uk/audio/firWindowing.html